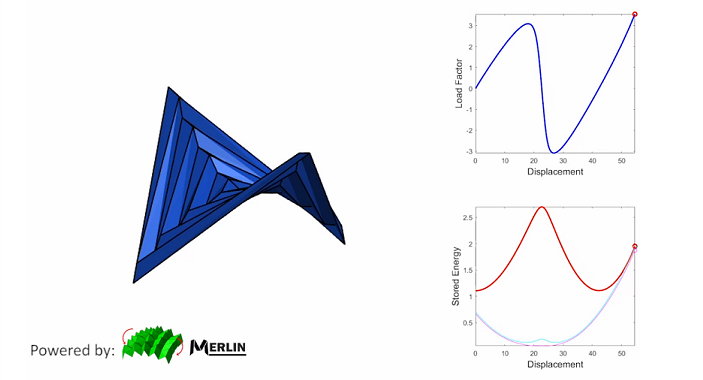
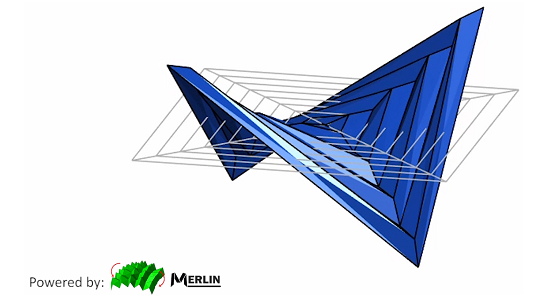
Professor Ke Liu, Prof. T. Tachi, and Prof. G. H. Paulino, show that an origami, folded from a flat sheet of paper via a discrete number of concentric squares (a hypar), is invariantly a hyperbolic paraboloid in the mathematical limit of the number of concentric squares, and it does not matter whether the concentric squares have uniform width or randomly distributed widths. Further, by connecting geometry and mechanics, they prove that a folded hypar has bistability between two symmetric configurations, which they harness to create multi-stable metasurfaces with programmable non-Euclidean geometries by tessellating the hypars.

The work was published in Nature Communications on September 17, 2019.

• View Full Text (PDF)

• View Supporting Information (PDF)